Back to ListTitle
Geometric learning
Lecturer
Pietro Pala, pietro.pala@unifi.it
Stefano Berretti, stefano.berretti@unifi.it
Content and organization
So far, research on Deep Learning techniques has mainly focused on data defined on Euclidean domains (i.e., grids). However, in a multitude of different fields, such as Biology, Physics, Network Science, Recommender Systems and Computer Graphics, one may have to deal with data defined on non-Euclidean domains (i.e., graphs and manifolds). The adoption of Deep Learning in these fields has been lagging until very recently, primarily since the non-Euclidean nature of data makes the definition of basic operations (such as convolution) rather elusive.
Geometric Deep Learning deals with the extension of DL techniques to graph/manifold structured data. In this course, we will introduce this area of research by presenting recent research advancements in DL applied to point clouds, graphs, meshes and manifolds. Example applications will be illustrated in laboratory sessions.
Content
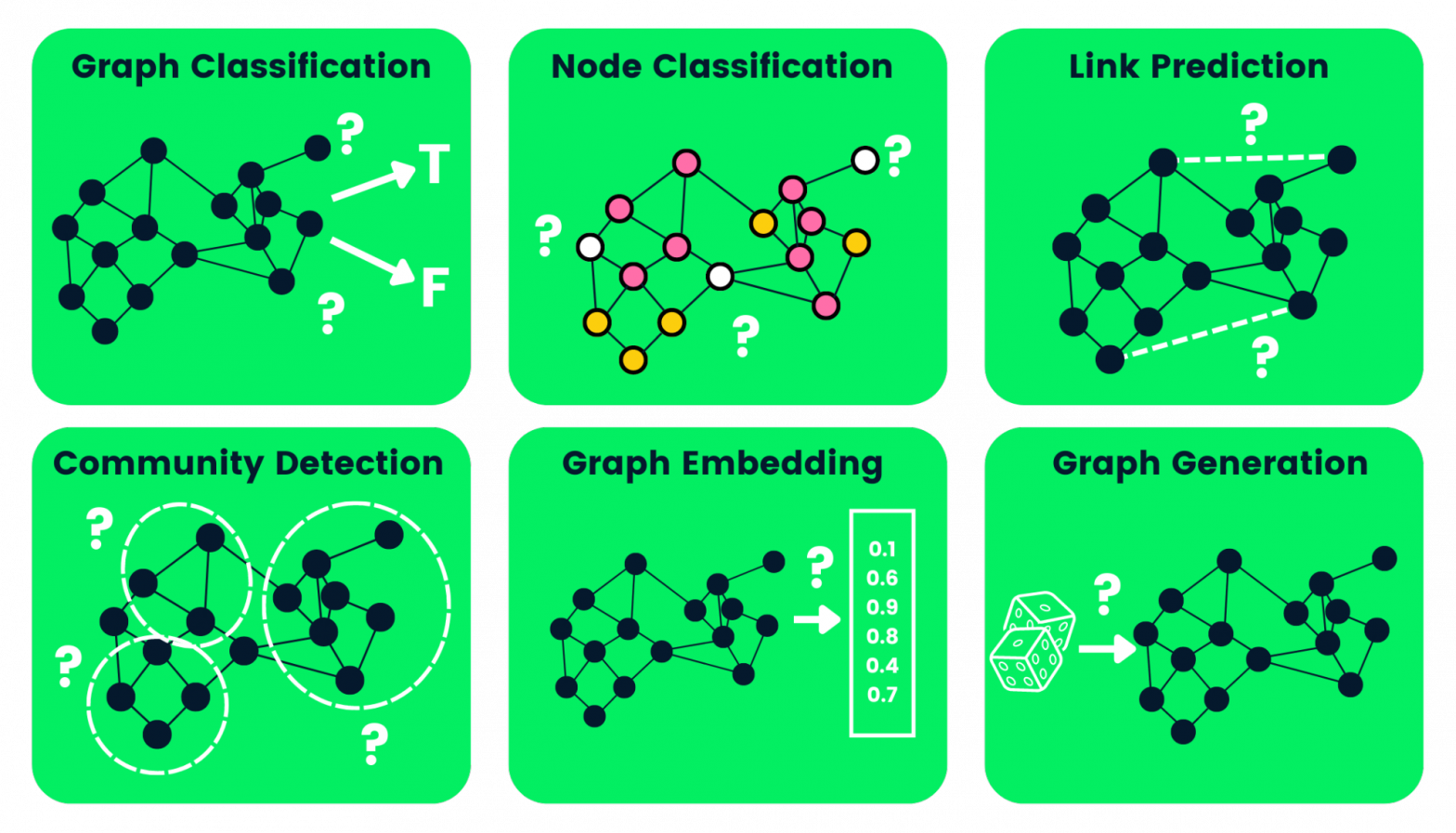
Convolutional Graph Neural Networks: Spatial and Spectral approaches
Graph Neural Networks message passing model
Attention in GNN
Graph pooling
Generalized convolutions: point cloud and meshes
Generative models and adversarial perturbations
Level
PhD
Course Duration
6
Course Type
Short Course
Participation terms
No registration fee.
Schedule
June 11, 10.00-13.00 CEST and June 12, 10.00-13.00 CEST
Language
English
Modality (online/in person):
Online, googleMeet
Host Institution
Other short courses
